Per-Object Distance Variation Filter

The per-object distance variation filter calculates the uniformity of a given object.

Category	Object Processing
Node
Parameters	Distance Method: which method to use to calculate the distance. See the Distance Classifier Filter for more information about the various distance methods. Output Configuration: whether to enable the optional output for the variance coefficient
Inputs	Objects: a list of objects as generated from an object detection filter Input Pixels: the input pixel data that should be used to determine the uniformity
Outputs	Standard Deviation: the standard deviation of the distances of the individual pixels from the object’s average spectrum Variance Coefficient: the standard deviation (see above) normalized by the mean of the distances

Effect of the Filter

The filter takes two inputs: an object list (typically directly from an object detection filter), and a image-based pixel input. The pixel input must have the same image structure that the image has the objects were initially detected on.

For each object it will perform the following algorithm:

It will generate an average spectrum of all of the pixels in the object.

For each pixel it will calculate the distance between that pixel and that average spectrum using the distance method specified in the parameters. (In the Mahalanobis case an inverse covariance matrix will be calculated for each object individually.)

It will then calculate the mean and standard deviation of the resulting distances of the object.

The standard deviation is always provided as the first output; the relative standard deviation is provided optional second output.

In terms of a formula, if the distance function is given by $d(\mathbf{x},\mathbf{y})$ , this filter calculates the resulting mean distance $\mu$ and standard deviation $s$ per object from the input spectra $\mathbf{s}_i$ via:

$\mu = \frac{1}{n} \sum_{i=1}^{n} d\left(\mathbf{s}_i, \frac{1}{n} \sum_{i=j}^{n} \mathbf{s}_j \right)$

$s = \sqrt{\frac{1}{n} \sum_{i=1}^{n} \left( d\left(\mathbf{s}_i, \frac{1}{n} \sum_{i=j}^{n} \mathbf{s}_j \right) - \mu \right)^2}$

The result of this filter can be used as an estimate as to how uniform a given object is.

Illustration with Artificial Data

Take the following input data for the object detector:

The detector would generate the following list of objects:

If the pixel input for the object is given by the following list of spectra:

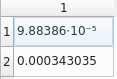
Then the per-object distance variation filter will return the following standard deviations for the objects (when the distance method is selected to be Cosine):

_images/perobjectdistancevariation_output.png

Handling of Training Data

Similar to the Per-object Averaging Filter this filter will produce a hidden data set where this operation is applied to the individual pixels of each group during training. This is done primarily for consistency; using a group-based classifier after this filter is likely not very useful.

Sequenced Operations (Line Cameras)

The object processing filter also works with line cameras (or in the case of hyperspectral cameras, Push Brooms). The processing framework will automatically keep enough of the input pixel data round in memory that once the line gets processed that causes the object detector to output the object, the pixels that belonged to the object remain accessible to this filter.