Principal Component Analysis Filter
Reduces the dimensionality of data via the Principal Component Analysis.
Category |
|
Node |
|
Parameters |
CutoffMethod: whether to determine the number of resulting dimensions of the PCA dynamically by variance (ByVariance, see below), or to fix the number of dimensions (Fixed) CutOffAdditionalVariance: when the dimensionality is determined dynamically, how much variance must the next principal component explain if it is still to be considered (range is from 0 to 1, where 1 is 100%) CutOffPrincipalComponents: when the dimensionality is determined dynamically, how much variance may the existing principal components explain to cause a cutoff of the rest (range is from 0 to 1, where 1 is 100%) MaxDimensionality: the maximum number of principal components to find in the dynamic case before forcing a cutoff Dimensionality: in the fixed case this specifies the number of principal components to find Scaling: how the resulting data should be scaled (see below) |
Inputs |
Input: the high-dimensional input data |
Outputs |
Output: the data projected onto the subspace |
Effect of the Filter
This filter may be used to reduce the dimensionality of the input data. During training it processes all input data that it was given (except for pixels that were marked as ignored) and tries to organzie the training data into principal components in order of the explained variance.
All data is then projected onto that subspace to reduce the dimensionality.
For example, if a data set with the following set of spectra is loaded and used in conjunction with the PCA:
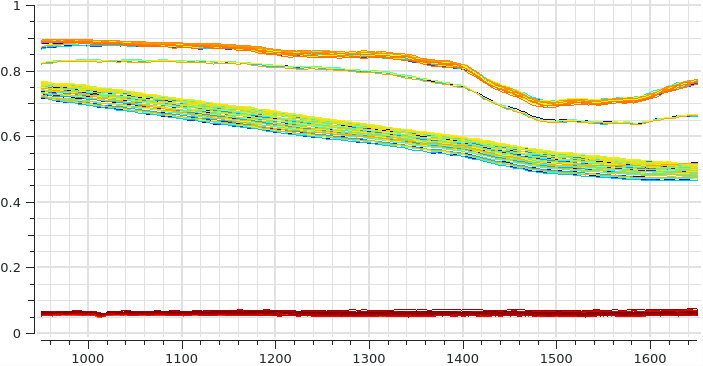
Then the PCA can easily separate the various different spectra, in this case with two latent vectors:
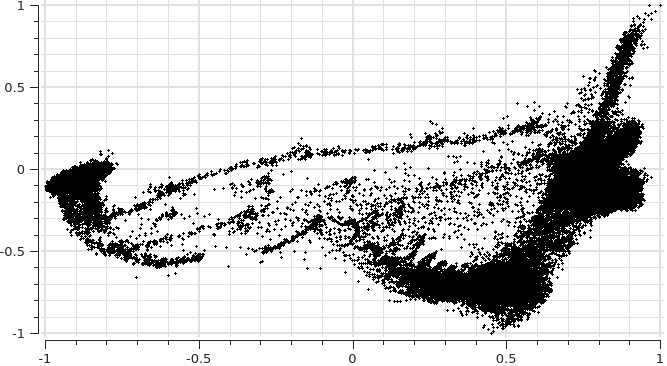
Fixed vs. By Variance Cutoff
The number of principal components used can either be fixed by the user (by selecting CutoffMethod to be Fixed), or it can be automatically determined.
When automatically determined there are three different cutoffs that are all checked after all possible principal components have been ordered in decreasing level of variance of the input data that they explain:
If the number of principal components reaches the maximum number as specified in the MaxDimensionality parameter, then the cutoff happens at this point
If the next principal component that would be added to the already existing list of principal components explains less variance than what the parameter CutOffAdditionalVariance requires, that component will not be included, and the algorithm will terminate at this point
If after adding a principal component the total variance that is now explained is larger than the parameter CutOffPrincipalComponents, the algorithm will terminate at this point
By using this dynamic cutoff method it allows the user to determine how much variance there actually is in the data, without fitting to noise that is present in the training data.
